Benutzer:tobit09/Stochastik3Stochastisches Modellieren für Einsteiger
 2. Ereignisse E 2. Ereignisse E  Inhaltsverzeichnis Inhaltsverzeichnis  4. Zufallsvariablen X 4. Zufallsvariablen X
3. Zähldichten 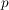 und Wahrscheinlichkeits-Verteilungen und Wahrscheinlichkeits-Verteilungen 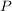
a) Zähldichten 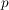
Nachdem ein stochastischer Vorgang durch eine Ergebnismenge 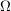 beschrieben ist, kann die zugehörige Zähldichte beschrieben ist, kann die zugehörige Zähldichte 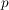 angegeben werden. angegeben werden. 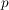 ist eine Vorschrift (Abbildung), die jedem Ergebnis ist eine Vorschrift (Abbildung), die jedem Ergebnis 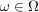 die Wahrscheinlichkeit von Ausgang die Wahrscheinlichkeit von Ausgang 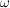 zuordnet. zuordnet.
Beispiel: Würfelwurf

Bekanntlich hat jede der Zahlen von 1 bis 6 beim Würfelwurf Wahrscheinlichkeit  , geworfen zu werden. Also: , geworfen zu werden. Also:
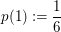 , , 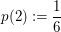 , , 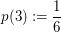 , , 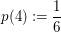 , , 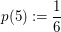 , , 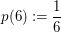
Kürzer: 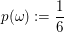 für alle für alle 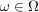
Aufgabe 7: Geben Sie eine geeignete Zähldichte für das Drehen des Glücksrades an, dessen eine Hälfte aus einem Nietenfeld und dessen andere Hälfte wiederum zur Hälfte aus einem Trostpreisfeld und einem Hauptpreisfeld besteht.
Lösungsvorschlag
b) Wahrscheinlichkeits-Verteilungen 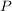
Die Zähldichte 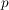 ordnet jedem Ergebnis ordnet jedem Ergebnis 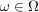 die Wahrscheinlichkeit von Ausgang die Wahrscheinlichkeit von Ausgang 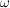 zu. Die zugehörige Wahrscheinlichkeits-Verteilung zu. Die zugehörige Wahrscheinlichkeits-Verteilung 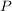 ordnet dagegen jedem Ereignis ordnet dagegen jedem Ereignis 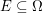 seine Wahrscheinlichkeit zu. seine Wahrscheinlichkeit zu. 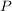 hängt mit hängt mit 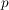 in folgender Weise zusammen: in folgender Weise zusammen:
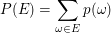
für alle 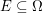 . .
Beispiel: Wie wahrscheinlich ist es, beim Werfen eines Würfels eine gerade Zahl zu würfeln?

Wir suchen die Wahrscheinlichkeit von 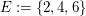 . .
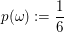 für alle für alle 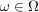 . .

Also beträgt die gesuchte Wahrscheinlichkeit  . .
Aufgabe 8: Wie wahrscheinlich ist es bei dem Glücksrad aus Aufgabe 7, keine Niete zu erdrehen?
Lösungsvorschlag
c) Laplace-Experimente
Ein Laplace-Experiment ist ein stochastischer Vorgang, bei dem alle Ausgänge 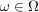 gleich wahrscheinlich sind. Diese Wahrscheinlichkeit jedes einzelnen Ergebnisses gleich wahrscheinlich sind. Diese Wahrscheinlichkeit jedes einzelnen Ergebnisses 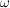 lautet in diesem Fall lautet in diesem Fall
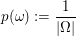 , ,
wobei 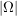 die Anzahl der Elemente von die Anzahl der Elemente von 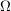 (also die Anzahl aller möglichen Ausgänge) bezeichnet. Weiter gilt im Falle eines Laplace-Experimentes (also die Anzahl aller möglichen Ausgänge) bezeichnet. Weiter gilt im Falle eines Laplace-Experimentes
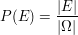
für alle Ereignisse 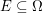 . .
Beispiel: Wie wahrscheinlich ist es, beim zweifachen Würfelwurf eine gerade Augensumme zu erhalten?

Gesucht ist die Wahrscheinlichkeit von
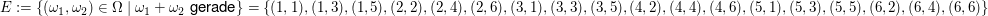 . .
Es liegt ein Laplace-Experiment vor (alle Paare 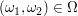 haben gleiche Wahrscheinlichkeit). haben gleiche Wahrscheinlichkeit).
(Also 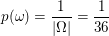 für alle für alle 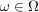 .) .)
Somit gilt 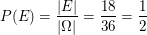 . .
Die gesuchte Wahrscheinlichkeit lautet also  . .
Aufgabe 9: Liegt in den folgenden Situationen jeweils ein Laplace-Experiment vor?
(i) 10-facher Münzwurf (mit einer fairen Münze)
(ii) Aus der Urne mit 3 schwarzen und einer weißen Kugel wird eine Kugel gezogen. 
(iii) Aus der Urne mit 3 schwarzen und einer weißen Kugel wird eine Kugel gezogen. 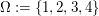 , wobei 1, 2 und 3 für die schwarzen Kugeln stehen und 4 für die weiße Kugel steht. , wobei 1, 2 und 3 für die schwarzen Kugeln stehen und 4 für die weiße Kugel steht.
Lösungsvorschlag
Hat man wie in den Teilen (ii) und (iii) von Aufgabe 9 die Wahl zwischen mehreren Ergebnismengen 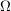 , von denen eine ein Laplace-Experiment darstellt, so sollte man diese wählen. Zum einen sind so die einzelnen Wahrscheinlichkeiten , von denen eine ein Laplace-Experiment darstellt, so sollte man diese wählen. Zum einen sind so die einzelnen Wahrscheinlichkeiten 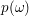 besser begründet oder lassen sich überhaupt nur so problemlos angeben. Zum Anderen lässt sich mit Laplace-Verteilungen wegen besser begründet oder lassen sich überhaupt nur so problemlos angeben. Zum Anderen lässt sich mit Laplace-Verteilungen wegen 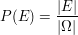 besser rechnen. besser rechnen.
| 