Benutzer:tobit09/Beweis-Anleitung Benutze-AnleitungWie führe ich einen Beweis?
 3. Wie zeige ich...? 3. Wie zeige ich...?  Inhaltsverzeichnis Inhaltsverzeichnis  5. Beispiele 5. Beispiele
4. Wie benutze ich...?
a) Wie benutze ich eine "und"-Aussage?
Eine Voraussetzung der Form  kannst du als zwei gleichzeitig bestehende Voraussetzungen kannst du als zwei gleichzeitig bestehende Voraussetzungen  und und 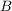 betrachten. betrachten.
Beispiel: Gleichheit von Mengen
b) Wie benutze ich eine "oder"-Aussage?
Eine Voraussetzung der Form  legt eine Fallunterscheidung nach legt eine Fallunterscheidung nach  und und 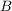 nahe. Zeige in beiden Fällen getrennt nacheinander die Behauptung. nahe. Zeige in beiden Fällen getrennt nacheinander die Behauptung.
Beispiele: Teilmengenbeziehung 1, Gleichheit von Mengen
c) Wie benutze ich eine "es folgt"-Aussage?
Eine Voraussetzung der Form 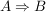 kannst du nutzen, indem du kannst du nutzen, indem du  zeigst und zeigst und 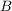 folgerst. folgerst.
Beispiel: Injektivität, Bilder und Urbilder
d) Wie benutze ich eine "genau dann, wenn"-Aussage?
Eine Voraussetzung der Form  liefert dir liefert dir 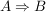 und und  , was du wie unter c) beschrieben nutzen kannst. , was du wie unter c) beschrieben nutzen kannst.
e) Wie benutze ich eine "nicht"-Aussage?
Bei einer Voraussetzung der Form 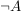 solltest du dir klar machen, was solltest du dir klar machen, was 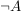 im konkreten Fall bedeutet: im konkreten Fall bedeutet:
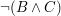 bedeutet bedeutet  . .
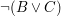 bedeutet bedeutet  . .
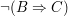 bedeutet bedeutet 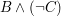 . .
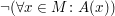 bedeutet bedeutet 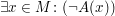 . .
 bedeute bedeute 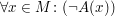 . .
Beispiel: Gleichheit von Mengen
f) Wie benutze ich eine "für alle"-Aussage?
Eine Voraussetzung der Form 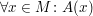 kannst du nutzen, indem du ein Element kannst du nutzen, indem du ein Element 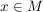 findest und auf findest und auf  für dieses Element schließt. für dieses Element schließt.
Beispiele: Surjektivität, Injektivität, Bilder und Urbilder
g) Wie benutze ich eine "es existiert"-Aussage?
Eine Voraussetzung der Form 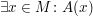 kannst du nutzen, indem du als zusätzliche Voraussetzung annimmst, dass ein Element kannst du nutzen, indem du als zusätzliche Voraussetzung annimmst, dass ein Element 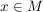 mit mit  gegeben ist. gegeben ist.
Beispiele: Surjektivität, Injektivität, Bilder und Urbilder
h) Wie benutze ich die Gleichheit zweier Objekte?
Eine Voraussetzung der Form 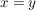 sagt dir, dass für jede wahre Aussage sagt dir, dass für jede wahre Aussage  auch auch  gilt und umgekehrt. gilt und umgekehrt.
Beispiel: Injektivität, Bilder und Urbilder
| 